Movimiento de proyectiles
Cualquier objeto que sea lanzado en el aire con una velocidad inicial
Por eso es importante explicar el movimiento de un proyectil como resultado de la superposición de un movimiento rectilíneo uniforme y uno uniformemente variado, estableciendo las ecuaciones de la curva representativa, tiempo de vuelo, tiempo máximo, altura máxima, alcance máximo, velocidad y coordenadas de posición en el plano.
¿Qué es un proyectil?
El movimiento de un proyectil es un ejemplo clásico del movimiento en dos dimensiones con aceleración constante. Un proyectil es cualquier cuerpo que se lanza o proyecta por medio de alguna fuerza y continúa en movimiento por inercia propia. Un proyectil es un objeto sobre el cual la única fuerza que actúa es la aceleración de la gravedad. La gravedad actúa para influenciar el movimiento vertical del proyectil. El movimiento horizontal del proyectil es el resultado de la tendencia de cualquier objeto a permanecer en movimiento a velocidad constante.
El término proyectil se aplica por ejemplo a una bala disparada por un arma de fuego, a un cohete después de consumir su combustible, a un objeto lanzado desde un avión o en muchas actividades deportivas (golf, tenis, fútbol, béisbol, atletismo etc.). L os fuegos artificiales y las fuentes del agua son ejemplos del movimiento de proyectiles . El camino seguido por un proyectil se denomina trayectoria . El estudio del movimiento de proyectiles es complejo debido a la influencia de la resistencia del aire, la rotación de la Tierra, variación en la aceleración de la gravedad.
La ciencia encargada de hacer el estudio del movimiento de los proyectiles se llama balística.
Experiencia de Galileo Galilei:
El hombre conocía las trayectorias parabólicas aunque no las denominaba así y experimentaba con tiros parabólicos (Por ejemplo, recuerde las destrezas de David frente a Goliat). Galileo fue el primero que dio una descripción moderna y cualitativa del movimiento de proyectiles dando las bases para su conocimiento y demostró que la trayectoria de cualquier proyectil es una parábola.
Galileo realizó un experimento con dos objetos: impulsó uno horizontalmente desde una mesa y dejó caer otro cuerpo desde el borde verticalmente. Al dejar caer un cuerpo A verticalmente
Lanzamiento horizontal
Una pelota de béisbol se proyecta horizontalmente en el vacío desde un punto O con velocidad
La trayectoria seguida por la pelota puede considerarse como el resultado de dos movimientos: Uno horizontal uniforme a lo largo del eje x y de velocidad constante
Ecuaciones de la velocidad
La componente horizontal de la velocidad
La componente vertical
La magnitud de la velocidad resultante V, viene dada en módulo por la expresión:
Para determinar la dirección del vector
| | Luego: |
| | Recordar que el vector velocidad siempre es tangente a la trayectoria descrita por la partícula |
Ecuaciones del desplazamiento
Como se puede notar el movimiento tiene simultáneamente un desplazamiento horizontal (
La ecuación de desplazamiento horizontal (X) en módulo, es la misma del movimiento rectilíneo uniforme puesto que la rapidez en ese sentido es constante
El desplazamiento vertical (y) en módulo se calcula como si el cuerpo se moviese en caída libre
La posición a lo largo del eje y, en el tiempo t.
El desplazamiento total (d) en módulo viene dado por:
La dirección del desplazamiento se obtiene aplicando la definición de tangente
El tiempo de vuelo (
Es el tiempo transcurrido desde el momento del lanzamiento hasta tocar el suelo.
| | Recuerde que la cantidad subradical será siempre positiva |
Ecuación de la Trayectoria
La idea consiste en demostrar que la trayectoria del proyectil es parabólica. En efecto, el desplazamiento horizontal para un cierto tiempo t viene dado por:
| | de donde : | |
Por otra parte, el desplazamiento vertical al mismo tiempo t es:
Como el tiempo para ambos desplazamientos es el mismo, podemos sustituir t de la ecuación (a) en tde la ecuación (b) quedando:
Como
| | que corresponde a la ecuación de una parábola. |
Ejemplo:
Un avión vuela con una velocidad horizontal constante de 600km/h a una altura de 6 km y se dirige hacia un punto que se encuentra directamente arriba de su objetivo ¿ Cuál es el ángulo de mira al que debe arrojarse un paquete de supervivencia para que llegue a su objetivo?
Solución:
Se escoge un referencial fijo respecto de la Tierra con su origen 0 en el punto que se suelta el paquete, cuya velocidad en el momento de ser soltado, es igual a la del avión.
De aquí que la velocidad inicial del paquete Vo sea horizontal y su magnitud sea de 600 Km/h. El ángulo de tiro es cero.
El tiempo de vuelo se calcula con la expresión
| R = | R = 5831,43 m = 5831,4 m = x |
De modo que el ángulo de mira f se define como
Lanzamiento inclinado
Consiste en estudiar el caso de una partícula o proyectil que se lanza con una velocidad inicial  , formando un ángulo q0 con la dirección horizontal. Su velocidad cambia constantemente debido a la acción del campo gravitatorio.
, formando un ángulo q0 con la dirección horizontal. Su velocidad cambia constantemente debido a la acción del campo gravitatorio.
Los componentes rectangulares de la velocidad inicial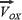 y
y 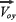 . (Los subíndices se utilizan para indicar los valores iniciales de
. (Los subíndices se utilizan para indicar los valores iniciales de  en cada uno de los ejes). Si no existiera la atracción gravitatoria, en tiempos t1, t2, t3, … ocuparía respectivamente posiciones tales como A, B, C, D, y el movimiento sería rectilíneo uniforme de velocidad constante
en cada uno de los ejes). Si no existiera la atracción gravitatoria, en tiempos t1, t2, t3, … ocuparía respectivamente posiciones tales como A, B, C, D, y el movimiento sería rectilíneo uniforme de velocidad constante  , Sin embargo como el proyectil está sometido a la fuerza de atracción gravitatoria, a la vez que se mueve según la recta AE, cae verticalmente, y al final de los tiempos indicados las posiciones del proyectil son respectivamente A', B',C,'D' … La curva que une estos puntos determina la trayectoria del proyectil, que corresponde a una parábola.
, Sin embargo como el proyectil está sometido a la fuerza de atracción gravitatoria, a la vez que se mueve según la recta AE, cae verticalmente, y al final de los tiempos indicados las posiciones del proyectil son respectivamente A', B',C,'D' … La curva que une estos puntos determina la trayectoria del proyectil, que corresponde a una parábola.
Cuando el cuerpo es lanzado forma un ángulo q0 con la horizontal y la única fuerza que actúa es la atracción gravitatoria. Luego en la dirección horizontal no existe aceleración, en tanto que en la dirección vertical el cuerpo está sometido a la acción de la fuerza de la gravedad y por ello, en dicha dirección se manifiesta un movimiento con aceleración constante. Por lo tanto, el movimiento del proyectil será el resultado de la composición de dos movimientos, uno con velocidad constante en el eje x o eje de las abscisas y otro con aceleración constante en el eje y o eje de las ordenadas.
El proyectil en su movimiento ascendente está dotado de un movimiento uniformemente retardado con aceleración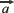 = - g. Se observa que la componente de la velocidad a lo largo del eje y (
= - g. Se observa que la componente de la velocidad a lo largo del eje y (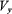 ), cuando el proyectil sube, va disminuyendo hasta hacerse igual a cero en el punto de máxima altura
), cuando el proyectil sube, va disminuyendo hasta hacerse igual a cero en el punto de máxima altura 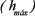 de la curva. A partir de este punto, cuando el proyectil empieza a bajar comienza un movimiento uniformemente acelerado
de la curva. A partir de este punto, cuando el proyectil empieza a bajar comienza un movimiento uniformemente acelerado 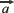 = g , luego la componente de la velocidad
= g , luego la componente de la velocidad 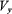 cambia de sentido y aumenta en magnitud a medida que el cuerpo continúa su caída libre. Se nota que durante todo
cambia de sentido y aumenta en magnitud a medida que el cuerpo continúa su caída libre. Se nota que durante todo
el movimiento, la componente horizontal de la velocidad a lo largo del eje horizontal (eje x )
se mantiene constante y por consiguiente el movimiento a lo largo de este eje es rectilíneo uniforme.
De acuerdo con lo anterior, como la partícula describe un movimiento que resulta de la superposición de un movimiento rectilíneo uniforme (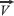 = constante) y un movimiento uniformemente variado (
= constante) y un movimiento uniformemente variado ( 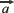 = constante) a lo largo de los ejes x y y, respectivamente, podemos encontrar las coordenadas de posición ( x,y ) del proyectil en cualquier instante t a partir de las siguientes ecuaciones.
= constante) a lo largo de los ejes x y y, respectivamente, podemos encontrar las coordenadas de posición ( x,y ) del proyectil en cualquier instante t a partir de las siguientes ecuaciones.
Ecuaciones de la velocidad en el momento del lanzamiento ( t = 0)
Se supone que se dispara un proyectil, con una velocidad inicial , formando con la horizontal un ángulo q0.
, formando con la horizontal un ángulo q0.
Las componentes del vector en las direcciones de los ejes vienen dadas en módulo por:
en las direcciones de los ejes vienen dadas en módulo por:
Ecuaciones de la velocidad para un instante después del lanzamiento
Cuando el proyectil ocupa una determinada posición en un instante t después de haber sido lanzado la velocidad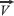 , tendrá una componente horizontal que se llama
, tendrá una componente horizontal que se llama 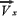 y una componente vertical que se llama
y una componente vertical que se llama 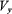 .
.
Ecuaciones del desplazamiento
El movimiento horizontal lo realiza el proyectil con velocidad constante, por lo que el desplazamiento horizontal x viene dado por la ecuación:
La magnitud de la componente horizontal de la velocidad se mantiene constante a través de todo el recorrido y vendrá dada por: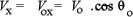
La magnitud de la componente vertical en cualquier instante viene dada por:
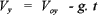
La magnitud de la velocidad en cualquier instante viene dada como: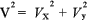
El ángulo que dicho vector forma con el eje horizontal representa la dirección de la velocidad y viene dado por: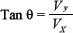
El movimiento vertical lo realiza con aceleración constante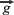 , dirigida hacia abajo, por lo que la ecuación del desplazamiento vertical y vendrá dada por:
, dirigida hacia abajo, por lo que la ecuación del desplazamiento vertical y vendrá dada por: 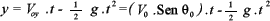
Si la anterior ecuación se resuelve para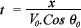 se obtiene:
se obtiene: 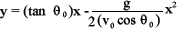
Esta ecuación es válida para ángulos de lanzamientos ubicados dentro del rango 0 < q0 < p / 2. La ecuación es válida para cualquier punto (x,y) a lo largo de la trayectoria del proyectil. Esta expresión es de la forma y = ax-bx2, que es la ecuación de una parábola que pasa por el origen. Se advierte que la trayectoria está completamente especificada si se conoce tanto la rapidez inicial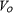 como el ángulo de lanzamiento q0.
como el ángulo de lanzamiento q0.
Ecuación del tiempo máximo
Se llama tiempo máximo, al tiempo empleado por el proyectil en alcanzar la altura máxima (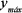 ).
).
A medida que el proyectil asciende va disminuyendo su velocidad hasta llegar un momento en que la misma se hace cero. Para ello hacemos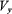 = 0 en la ecuación:
= 0 en la ecuación:
Ecuación de la altura máxima (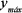 )
)
La altura máxima se obtiene haciendo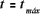 en la ecuación
en la ecuación 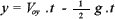
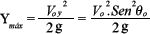
Ecuación del tiempo de vuelo (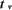 )
)
El tiempo de vuelo es el tiempo transcurrido por el proyectil desde su punto partida.
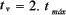
Alcance horizontal ( R ): Es el desplazamiento horizontal en el tiempo de vuelo.
Ejemplo:
José Manuel Rey, un notable futbolista de la Vinotinto patea el balón con un ángulo de inclinación sobre la horizontal de 37º y con una velocidad inicial de 20 m/seg. A 36 m del punto de partida se encuentra un vertical de la Portería con el cual choca la esférica. ¿A que altura del poste respecto a la horizontal pega el balón?
Solución:
Solución
Los componentes rectangulares de la velocidad inicial
Cuando el cuerpo es lanzado forma un ángulo q0 con la horizontal y la única fuerza que actúa es la atracción gravitatoria. Luego en la dirección horizontal no existe aceleración, en tanto que en la dirección vertical el cuerpo está sometido a la acción de la fuerza de la gravedad y por ello, en dicha dirección se manifiesta un movimiento con aceleración constante. Por lo tanto, el movimiento del proyectil será el resultado de la composición de dos movimientos, uno con velocidad constante en el eje x o eje de las abscisas y otro con aceleración constante en el eje y o eje de las ordenadas.
El proyectil en su movimiento ascendente está dotado de un movimiento uniformemente retardado con aceleración
el movimiento, la componente horizontal de la velocidad a lo largo del eje horizontal (eje x )
se mantiene constante y por consiguiente el movimiento a lo largo de este eje es rectilíneo uniforme.
De acuerdo con lo anterior, como la partícula describe un movimiento que resulta de la superposición de un movimiento rectilíneo uniforme (
Ecuaciones de la velocidad en el momento del lanzamiento ( t = 0)
Se supone que se dispara un proyectil, con una velocidad inicial
Las componentes del vector
| | (Componente Horizontal) |
| | (Componente Vertical) |
Cuando el proyectil ocupa una determinada posición en un instante t después de haber sido lanzado la velocidad
Ecuaciones del desplazamiento
El movimiento horizontal lo realiza el proyectil con velocidad constante, por lo que el desplazamiento horizontal x viene dado por la ecuación:
| |
La magnitud de la componente horizontal de la velocidad se mantiene constante a través de todo el recorrido y vendrá dada por:
La magnitud de la componente vertical en cualquier instante viene dada por:
La magnitud de la velocidad en cualquier instante viene dada como:
El ángulo que dicho vector forma con el eje horizontal representa la dirección de la velocidad y viene dado por:
El movimiento vertical lo realiza con aceleración constante
Si la anterior ecuación se resuelve para
Esta ecuación es válida para ángulos de lanzamientos ubicados dentro del rango 0 < q0 < p / 2. La ecuación es válida para cualquier punto (x,y) a lo largo de la trayectoria del proyectil. Esta expresión es de la forma y = ax-bx2, que es la ecuación de una parábola que pasa por el origen. Se advierte que la trayectoria está completamente especificada si se conoce tanto la rapidez inicial
Ecuación del tiempo máximo
Se llama tiempo máximo, al tiempo empleado por el proyectil en alcanzar la altura máxima (
A medida que el proyectil asciende va disminuyendo su velocidad hasta llegar un momento en que la misma se hace cero. Para ello hacemos
| |
Ecuación de la altura máxima (
La altura máxima se obtiene haciendo
Ecuación del tiempo de vuelo (
El tiempo de vuelo es el tiempo transcurrido por el proyectil desde su punto partida.
Alcance horizontal ( R ): Es el desplazamiento horizontal en el tiempo de vuelo.
Ejemplo:
José Manuel Rey, un notable futbolista de la Vinotinto patea el balón con un ángulo de inclinación sobre la horizontal de 37º y con una velocidad inicial de 20 m/seg. A 36 m del punto de partida se encuentra un vertical de la Portería con el cual choca la esférica. ¿A que altura del poste respecto a la horizontal pega el balón?
Solución:
Solución
| | q0= 37º | X = 36 m |
| | | |
La posición se denota por la ecuación:
| | Y = 2,19 = 2,2 m |